结果和讨论

界面行为、临界胶束浓度和表面过剩

图1恒定2 mM浓度下Mega-10和DPS的界面张力（γ）变化与α-CD浓度的关系图

图1显示了2 mM Mega-10和DPS溶液的界面张力（γ）随不同α-CD浓度的变化。两种表面活性剂溶液的界面张力值均随α-CD浓度的增加而增加。这种行为表明α-CD与Mega-10和DPS形成包合物，这些包合物没有任何表面活性。在没有α-CD的情况下，不同浓度的α-CD的界面张力对应于γ值，这证实了CD本身不具有表面活性（数据未显示）。图2显示了Mega-10和DPS（αDPS=0.8）混合体系在不同α-CD浓度下的总表面活性剂浓度的γvs.log曲线。每条曲线显示与cmc对应的断点。在图2中，由于α-CD中加入了表面活性剂单体，通过降低本体中的游离表面活性剂单体浓度延迟了胶束形成过程，因此每条曲线也移向更高的表面活性剂浓度。此外，cmc以上表面活性剂的γ值与α-CD浓度无关（图2）。这表明表面活性剂与α-CD形成的包合物不参与界面吸附。在α-DPS=0.0、0.2、0.4、0.6和1.0时，在不存在和存在2-8mmα-CD浓度的情况下，获得了类似的曲线图（数据未显示）。Mega-10和DPS的α-CD浓度依赖性cmc值如图3所示。图3清楚地显示了cmc和α-CD浓度之间的线性关系。这一行为是表面活性剂和α-CDs之间形成包合物的另一个迹象，导致表观cmc值增加。纯Mega-10（5.75 mM）和DPS（2.57 mM）测定的cmc值与报告的文献值一致[24–26]。

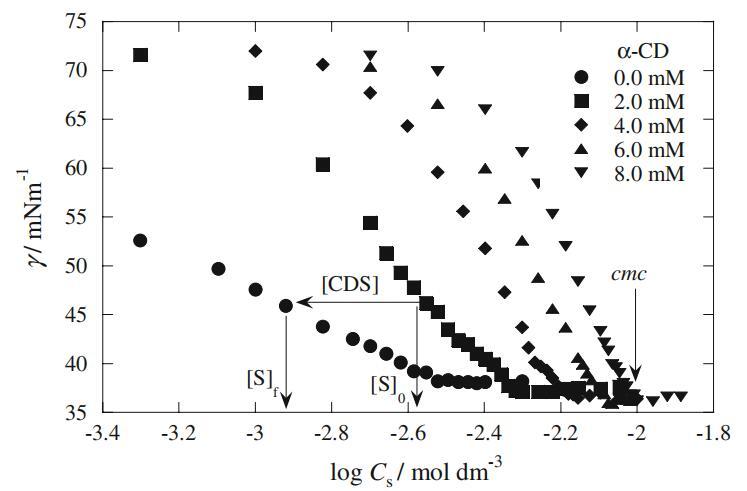
图2界面张力γ与对数Cs/mol dm的曲线图−不同α-CD浓度下Mega-10+DPS混合系统的α-DPS的3=0.80

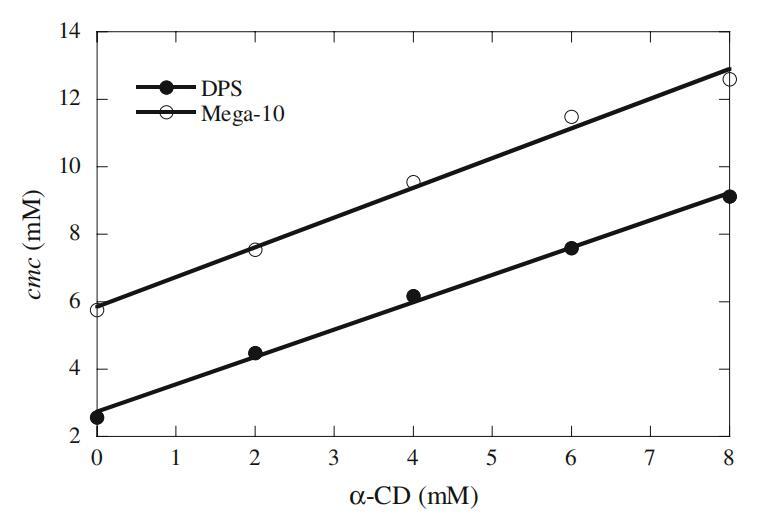
图3 Mega-10和DPS cmc依赖于α-CD浓度的曲线图

根据γ与log Cs/mol dm的曲线图−3，我们评估了纯表面活性剂和混合表面活性剂在空气-水界面上的界面吸附参数，在没有和存在不同的α-CD浓度的情况下。表面活性剂在cmc下的表面过量值Γmax表示表面活性剂在空气-水界面上的吸附量。稀溶液的表面过剩值可根据吉布斯方程确定，如下[27]：

式中，γ、C、R、T和P为界面张力、表面活性剂浓度、理想气体常数、温度和压力。纯系统和混合系统的Γmax值如图4所示。纯Mega-10和DPS分子的Γmax值与文献报道的值一致[26,28]。图4显示Mega-10的Γmax值略高于DPS。这一结果表明，与DPS相比，Mega-10分子在空气-水界面以更紧凑的形式排列。两种表面活性剂的Γmax值随着α-CD量的增加而减小，表明表面活性剂物种从界面上的解吸（图4）。这种行为是表面活性剂与α-CD之间存在相互作用的另一个证据。对于Mega-10和DPS在不同DPS摩尔分数（αDPS）下的二元混合物，Γmax值随着DPS量的增加而减小，表明DPS在界面上吸附后形成混合单层。

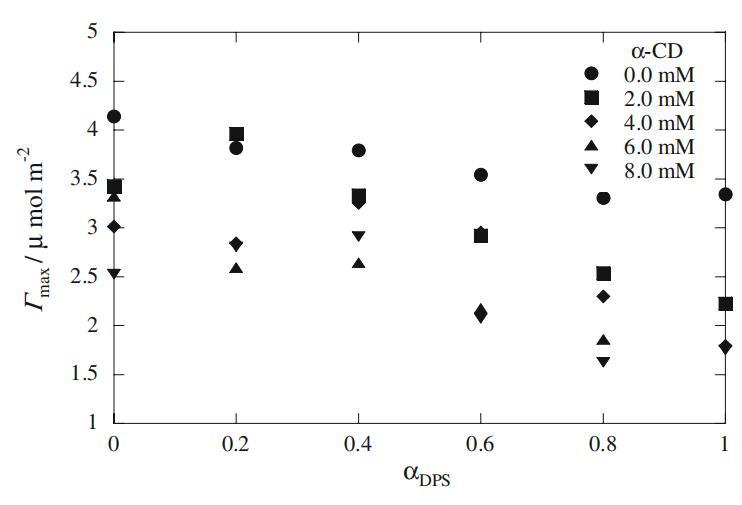
图4 Mega-10+DPS混合体系在水中和不同α-CD浓度下的表面过剩（Γmax）与α-DPS的曲线图

根据cmc值，我们评估了纯表面活性剂系统和混合表面活性剂系统在不存在和存在α-CD的情况下的胶束化标准自由能（数据未显示）[27]，随后，通过胶束转移标准自由能评估添加剂对胶束化的影响(∆GM，tr 0），从水相到含有α-CD的水相[19]。这些值如图5所示，在不同α-CD浓度下，在整个DPS摩尔分数范围内为正值，表明α-CD的存在使胶束形成不利。此外，这些值随着α-CD浓度的增加而线性增加，在高α-CD浓度下斜率更高，表明混合胶束的形成延迟。

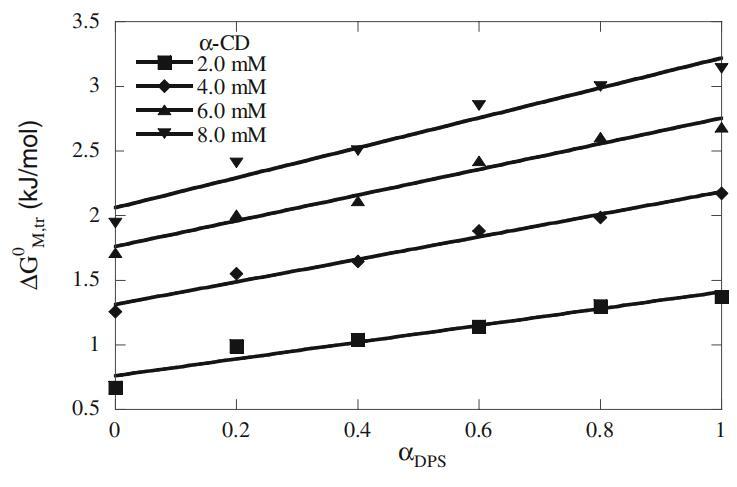
图5：试验结果的曲线图∆不同浓度α-CD中Mega-10+DPS的GM、tro和αDPS。实线表示最佳线性拟合

关联常数（Ka）

为了进一步探索α-CD-Mega-10和α-CD-DPS之间的相互作用，我们根据γ与表面活性剂浓度曲线的冰前浓度范围，假设化学计量比为1:1，评估了表面活性剂/α-CD络合物的缔合常数（Ka）。表面活性剂-镉络合物（S/CD）的整体表达式如下[13]：

其中，CD/S、[S]f、[CD]f、CD0和S0分别为包合物、游离表面活性剂、游离CD、总CD和总表面活性剂浓度。通过组合和重新排列等式。9-11，我们得到了以下关系式：

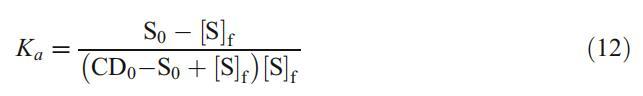
公式12的重新排列给出了以下等式：

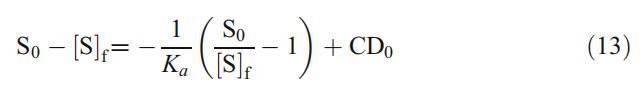
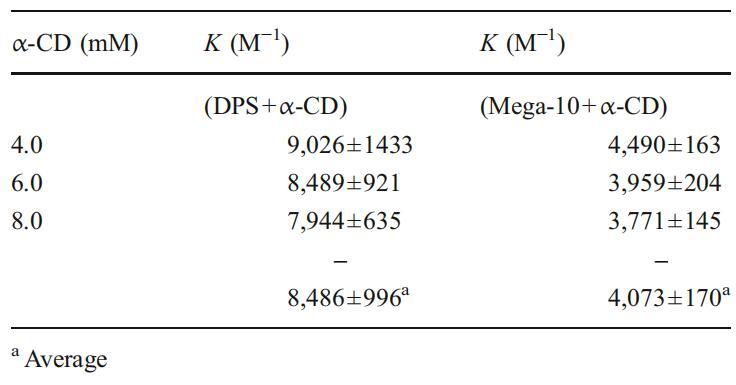
根据γ图确定的游离表面活性剂浓度（例如，见图2）。在存在CD的情况下，前冰层区域中特定γ值下的总单体表面活性剂浓度（S0）的增加是表面活性剂结合到CD的量的度量，即S0-[S]f=CD。从公式13可以看出，S0-[S]f应与S0/[S]f或S0/[S]f-1具有斜率的线性关系−1/Ka。我们已获得等式13的线性图（未显示数据）。表1列出了Mega-10+α-CD和DPS+α-CD包合物在不同α-CD下的Ka值。就两个客体分子与CD的缔合总结合能而言，缔合常数仅偏离约12%，对应的结合能差异仅为1.4%，因此可以认为是相当可比的。从Ka值来看，DPS分子与α-CD的相互作用似乎比Mega-10更强烈，因为烷基链稍长，极性头基团体积较小（以防止空间位阻）。由于疏水相互作用（与Mega-10相比，DPS中的冷冻水外壳更大）和范德华相互作用的增加，较长的碳链将提供更大的驱动力。此外，亲水性头部基团的结构可通过与环糊精边缘的醇的氢键作用，具有额外的络合物稳定性。表面活性剂-镉络合物的结构还通过2D NMR进行了研究，并在手稿的后半部分进行了介绍。Satake等人测定了α-CD和十二烷基磺酸钠、十二烷基氯化铵、十二烷基三甲基氯化铵、十二烷基氯化吡啶和十二烷基苯磺酸钠包合物2140 M的Ka值−12270米−12480米−12800米−15730米−1.分别为[14]。参考文献[7]给出了绑定常数评估的详细概述。

表1不同α-CD浓度下α-CD与DPS和Mega-10的1:1包合物的缔合常数（Ka）值

核磁共振

为了证实DPS-α-CD复合物的Ka值与Mega-10-α-CD复合物的Ka值具有可比性，我们进行了NMR测量，其中我们用α-CD滴定了表面活性剂的冰前浓度。图6显示了通过NMR用α-CD滴定表面活性剂的数据。将NMR滴定数据拟合至等式6，得出结合常数Ka为286±16 M−1表示Mega-10和α-CD之间的相互作用，Ka为729±8 M−1用于DPS与α-CD之间的相互作用。这里，就两个客体分子与镉的缔合总结合能而言，缔合常数仅偏离约14%，因此可以认为是相当可比的，并且与从界面研究中获得的缔合常数很好地对应。然而，核磁共振滴定得到的绝对Ka值与界面张力数据得到的值不同。上述差异也已在前面描述过[14,29,30]。

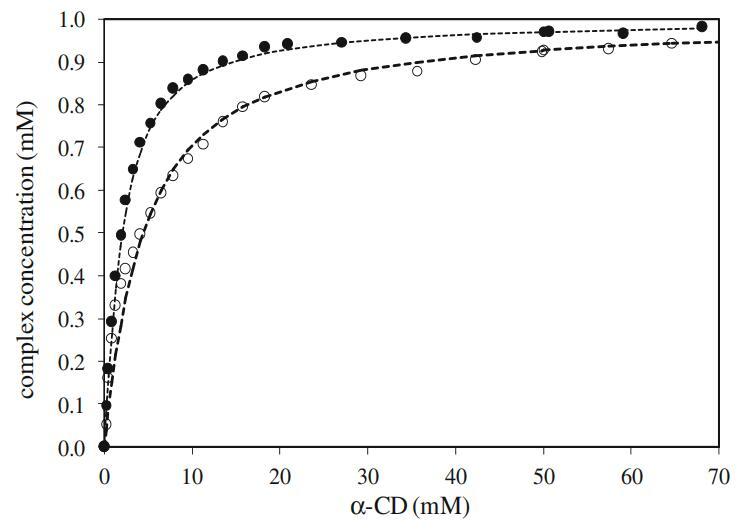
图6核磁共振滴定数据。绘制了镉表面活性剂复合物的浓度与镉浓度的关系图。表面活性剂浓度保持恒定在1mm。虚线表示最佳拟合。填充圆和开放圆分别表示DPS-α-CD系统和Mega-10-α-CD系统的数据

图7a显示了α-CD、DPS和Mega-10的示意图，以简化表面活性剂原子与CD原子的相互作用。2DROESY数据证明表面活性剂的烷基链包含在α-环糊精的疏水腔中。光谱如图7b和c所示。可以看到表面活性剂共振与位于环糊精空腔内的HIII、HV和HVI共振的交叉峰。未观察到分子（HI、HII和HIV）外部与环糊精原子的相互作用。对于这两种表面活性剂，与HIII和HV的相互作用似乎覆盖了从末端甲基到H3的整个烷基链。这意味着几个不同的复杂几何形状和穿透深度之间的快速交换。在镉原子和亲水性头基之间没有观察到相互作用。

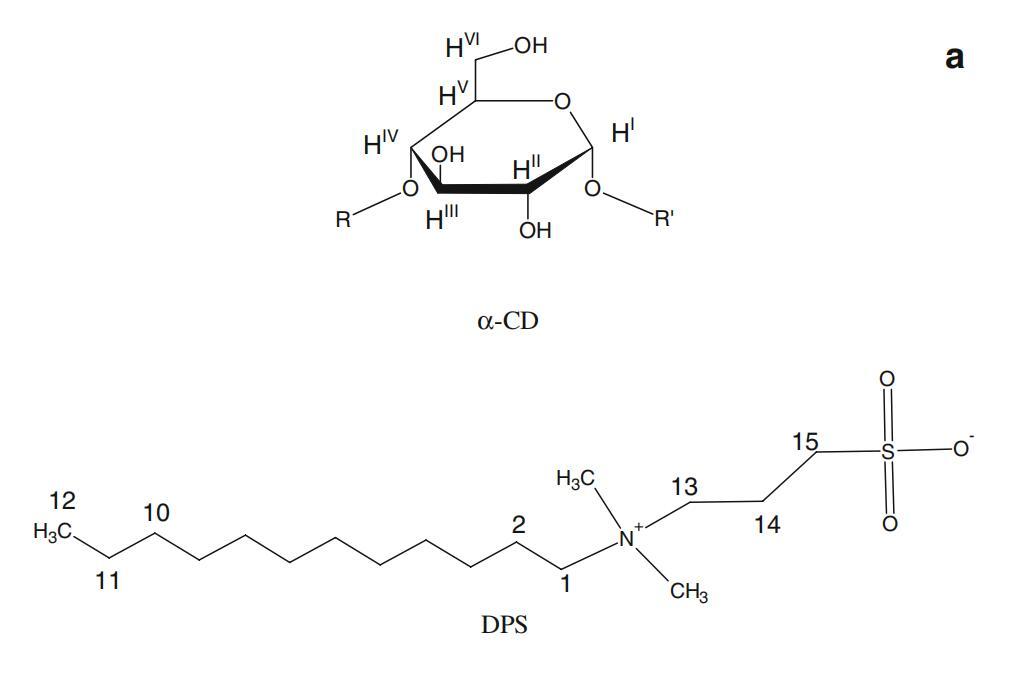
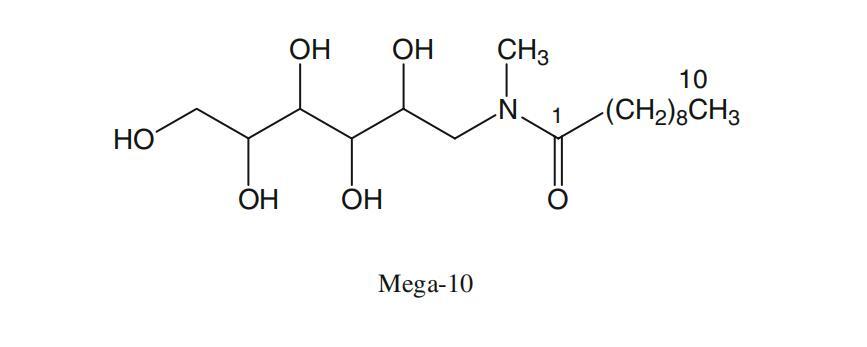
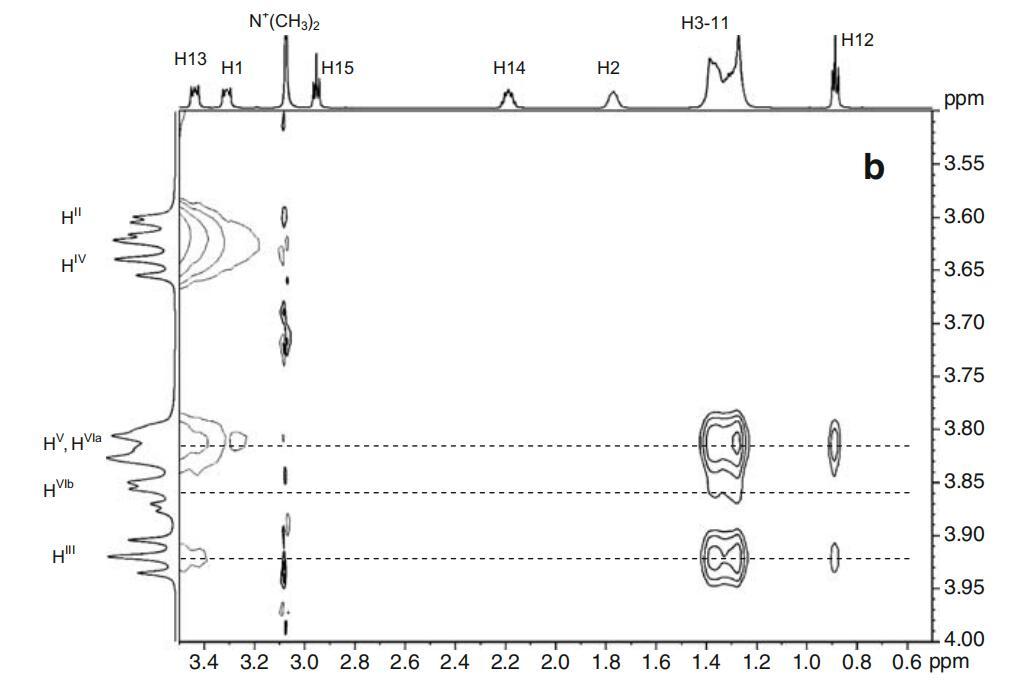
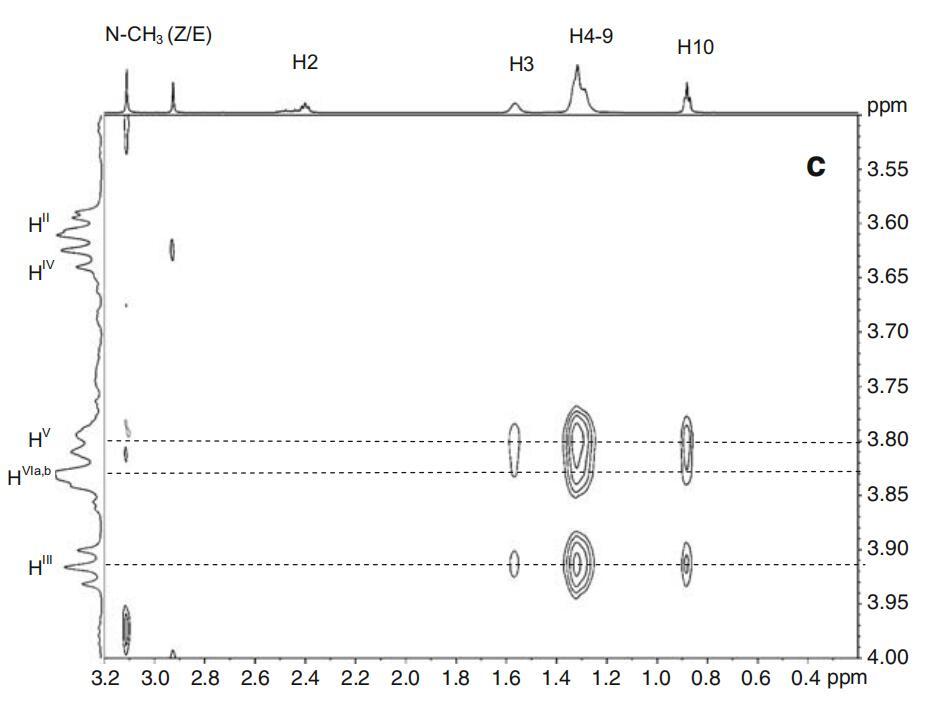
图7α-CD（所示为一个吡喃葡萄糖苷单元）、DPS和Mega-10的示意图。表面活性剂和α-CD的2D-ROESY光谱的关注区域。阿拉伯数字表示表面活性剂原子，而罗马数字表示CD原子。b为DPS-α-CD系统。Mega-10-α-CD系统的c

混合胶束的形成及相互作用参数

图8显示了Mega-10和DPS二元混合物在纯水和不同α-CD浓度（2–8 mM）下的混合cmc值。从图8可以清楚地看出，α-CD中的混合cmc值高于纯水中的值，并且这些值随着α-CD浓度的增加而增加。为了评估混合胶束的行为，即混合胶束是否表现出理想或非理想行为，我们使用了伪相分离模型[31]。简言之，根据该模型，胶束被认为是宏观相，与含有相应单体的溶液相平衡。对于表面活性剂的理想二元混合物，cmc由等式[31]关联

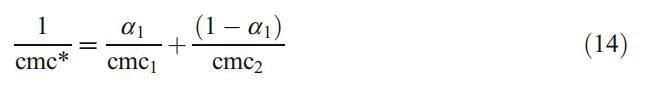
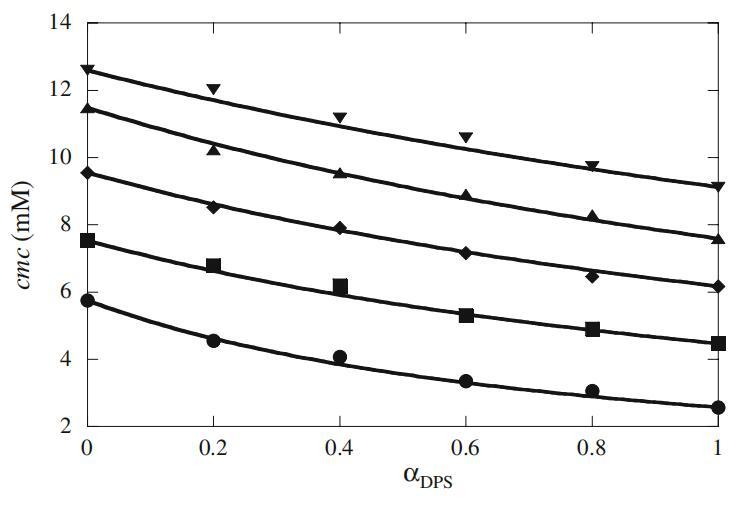
图8 Mega-10+DPS混合系统的混合临界胶束浓度（cmc）与αDPS的曲线图。填充圆、正方形、菱形、三角形和反向三角形分别表示存在0（填充圆）、2（填充正方形）、4（填充菱形）、6（填充三角形）和8（填充反向三角形）mMα-CD时的实验cmc。实线表示理想的cmc

由于二元混合物的组分在结构上彼此不同，因此由于头部和尾部基团的不同，预计会出现非理想行为。在不存在和存在不同α-CD浓度的情况下，在整个混合范围内，实验cmc值接近理想cmc*值，表明混合胶束的形成在本质上接近理想（图8）。α、β和γ-CDs与离子表面活性剂混合物的理想行为相似[19–21]。

这些结果已通过使用规则溶液理论得到进一步证实，该理论不仅表征了混合胶束中的相互作用参数bmic 12，而且还解释了与理想的偏差[32]。X1是胶束中DPS的摩尔分数，可根据以下方程式迭代计算：

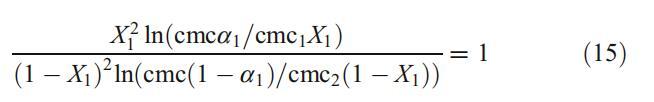
根据X1值，可通过以下方程式计算相互作用参数bmic 12：

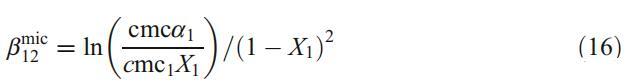
bmic 12值表明两种表面活性剂之间的相互作用程度，从而导致偏离理想行为。bmic 12的负值和正值分别表明混合胶束中两种表面活性剂之间的吸引和排斥作用。对于理想混合，bmic 12值应接近于零。在2和8 mMα-CD下，为当前二元混合物计算的bmic 12值分别为0.32和0.21。这些值非常接近在水系统中评估的值0.23。参考文献[22,23]列出了不同表面活性剂混合物相互作用参数的详细概述。由于α-CD存在时bmic 12值没有显着变化，且这些值接近于零，表明混合胶束的形成在本质上接近理想。

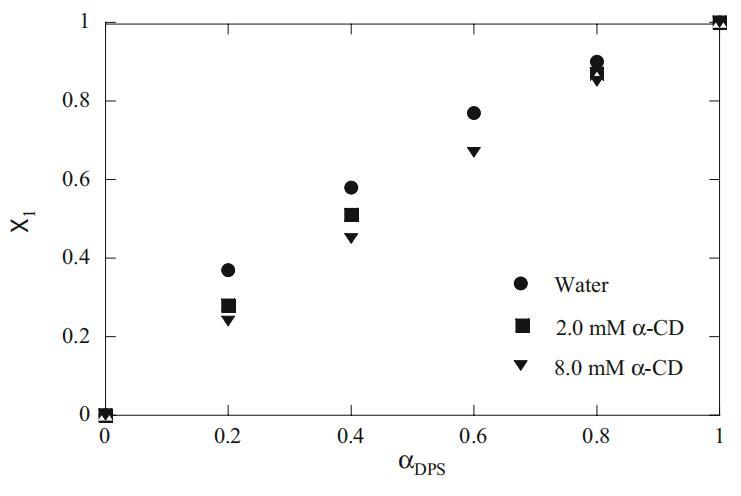
图9 Mega-10+DPS混合体系在水中和不同α-CD浓度下的胶束（X1）与α-DPS的曲线图

根据方程式15，我们计算了在不存在和存在α-CD的情况下当前二元混合物的胶束组成（X1）。图9显示了混合胶束（X1）和体积摩尔分数（α1）中表面活性剂的组成。从图9可以得出结论，在αDPS=0.2时，混合胶束中DPS的组成接近40%。存在α-CD时的X1值始终低于水的X1值。这种行为可能反映出α-CD通过降低其结合最强的表面活性剂的量来改变成分（见Ka值）。一般来说，CDs不与胶束相互作用，但CDs可能通过与溶液中的表面活性剂相互作用影响胶束的组成，从而改变胶束的平衡和组成。荧光各向异性为了研究混合胶束中两种不同组分的行为，我们还使用RB作为荧光探针进行了偏振荧光测量。这种探针在胶束介质中已经得到了很好的表征[33]。探针荧光发射的去极化程度是其激发态寿命期间旋转扩散的度量。荧光各向异性（r）通过Perrin方程与探针周围的粘度相关，如下[34]：

其中r0是在没有旋转自由度的情况下获得的发射各向异性的极限值，k是波尔兹曼常数，T是温度，τ是荧光团激发态的平均寿命，V是探针的有效分子体积，h是探针周围的粘度。从等式17可以看出，r值越高，刚性越高，反之亦然。

在这项工作中，我们研究了RB与表面活性剂-α-CD-水三元体系的详细相互作用，以便系统地研究RB的极化行为。在进入胶束介质之前，我们排除了RB与水溶液和水溶液α-CD介质中前冰层表面活性剂浓度（1 mM）的结合行为。图10显示了在冰层前表面活性剂浓度下，Mega-10和DPS的RB各向异性行为。在水中和存在α-CD（8mm）的情况下，我们未观察到表面活性剂RB的右旋值有任何显着变化。从图10获得的结果意味着探针RB不与表面活性剂单体、环糊精和α-CD表面活性剂包合物结合。在这些初始测量之后，我们将我们的实验方法扩展到胶束介质，以观察RB的各向异性行为。图11显示了纯表面活性剂以及Mega-10和DPS二元混合物（15mm）的α-CD（2-8mm）依赖性各向异性行为。从图11可以得出一些有趣的结论。首先，图11清楚地表明，在水介质中，纯Mega-10的胶束比DPS的胶束具有更高的微粘度。这种行为可以用表面活性剂分子在胶束中的堆积排列来解释，表明Mega-10胶束中的堆积比DPS胶束中的更紧密。对于二元混合物，r值随着DPS（αDPS）摩尔分数的增加而减小，这表明DPS被诱导到混合胶束中产生的刚性结构较低（参见图11中最左边的图例）。其次，在DPS的每摩尔分数下，r值随α-CD浓度的增加而线性减小。尽管随着α-CD浓度的增加，在αDPS=0.0时，r值的下降更为瞬时。我们注意到，r值的瞬时降低是由于胶束浓度的降低。为了证实这一结果，我们在20 mM浓度下对αDPS=0.0（即Mega-10）进行了各向异性测量，图12中绘制了Mega-10的观测r值，并与15 mM浓度下的αDPS=1.0（即DPS）进行了比较。正如我们所见，随着α-CD浓度的增加，Mega-10（20 mM）的r值没有瞬时下降，这表明图11中r值的急剧下降是由于胶束浓度的降低。DelaCruz等人研究了RB衍生物与阴离子、阳离子和非离子表面活性剂的相互作用，并得出结论，RB衍生物的酯链的电荷和长度控制着与不同胶束系统的相互作用[35]。

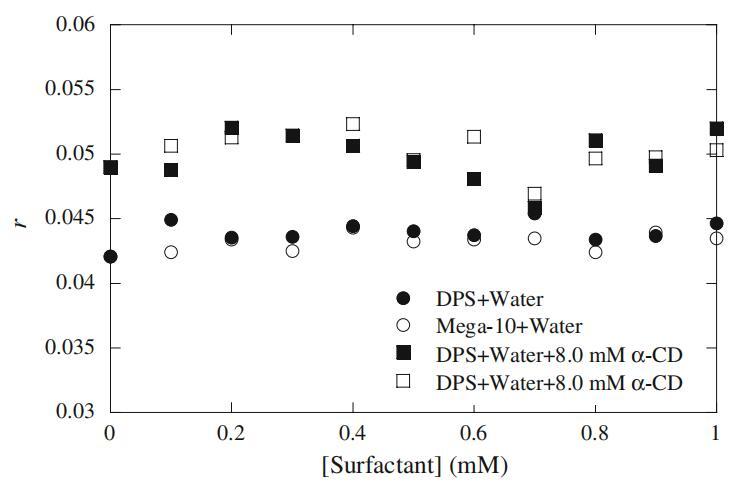
图10水和不同α-CD浓度下荧光各向异性r与前冰层表面活性剂浓度的曲线图

图11不同αDPS下荧光各向异性r与α-CD浓度的关系图

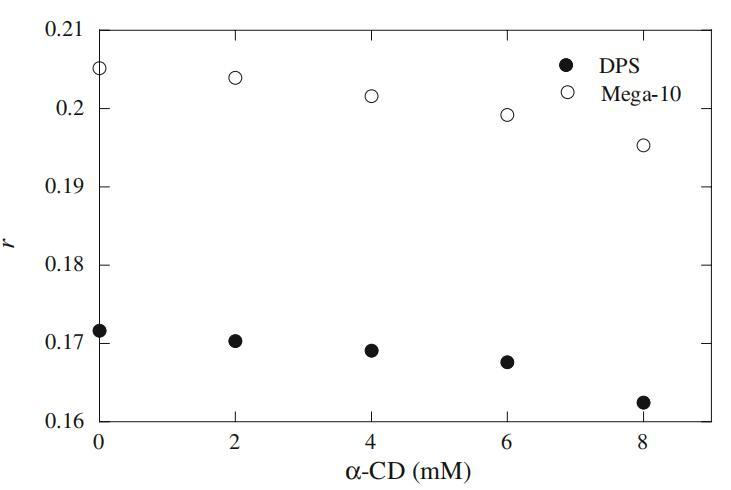
图12恒定表面活性剂浓度（Mega-10，20 mM和DPS，15 mM）下荧光各向异性r与α-CD浓度的关系图