摩登7平台合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
推荐新闻Info
-
> 水、常温液态金属等9种流体对液滴碰撞壁面影响的数值研究(三)
> 水、常温液态金属等9种流体对液滴碰撞壁面影响的数值研究(二)
> 水、常温液态金属等9种流体对液滴碰撞壁面影响的数值研究(一)
> 弹簧秤测量水的表面张力系数实验装置改进措施及效果
> 电晕对BOPP薄膜表面张力、化学结构、元素组成的影响
> 半泡法测定液体表面张力系数理论、实验设计
> 全氟庚烷端基聚丙烯酸(FPAA)合成方法及水溶液表面张力测定
> 纯聚苯胺LB膜和聚苯胺与乙酸混合的LB膜制备、NO₂气体敏感特性研究(下)
> 纯聚苯胺LB膜和聚苯胺与乙酸混合的LB膜制备、NO₂气体敏感特性研究(上)
> 不同相对两亲面积的Janus颗粒在油气表面性质和泡沫性能对比(三)
表面与界面物理力学
来源:科技千里眼 浏览 2827 次 发布时间:2022-06-20
今天咱们一同进入一个新的领域——【表面与界面物理力学】。
那么就从我们最常听说的名词——“表面张力”入手吧。

先来点准备知识——
表面与界面
表面(surface)是指【凝聚相】与【气体/真空】之间的分界面。
界面(interface)是指【凝聚相】与【凝聚相】之间的分界面。
凝聚相,可以理解为“固相+液相”。

表面能——形成表面的代价
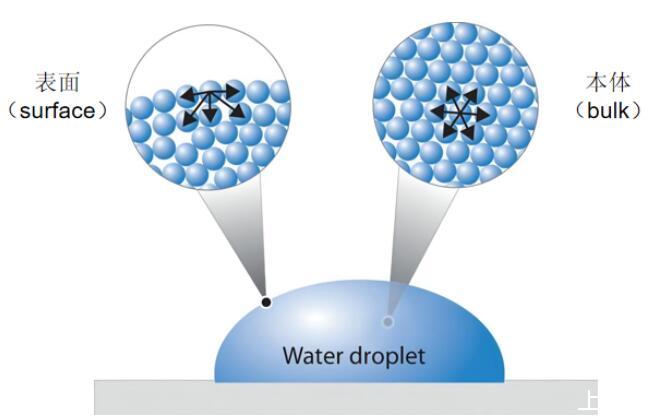
分子在材料的本体(bulk)中,四面八方都有其它的小伙伴,形成均匀的作用力和距离。
但是,表面的出现,使得一些分子变得不同,它们的外侧是气体或真空,几乎没有作用力,这使得表面上的分子“很不安分”,产生了额外的能量——表面能。
如何理解“表面能”呢?
比如,你把一块巧克力掰成了两半,巧克力发生的变化仅仅是增加了两个表面,而你掰的过程必须消耗掉能量E,因此每个表面的表面能就是E/2。

所以,表面能代表的是巧克力与空气的差异;同理,所谓“界面能”,就是表征界面两侧两种物质的差异,差异越大,界面能越大。
表面张力——减少表面能的努力
自然界的大道之一,就是“最小能量原理”。一个液滴,会自发地寻找能量最小的形状,这里的能量就是表面能,而在表面上的作用力就是表面张力。
太空无重力下的汞滴,会自发形成一颗完美的圆球;空中漂浮的肥皂泡,也会自发地形成一个个球形薄膜——

因为,在相同体积的物体中,球的表面积是最小的,物质会自发地趋向于表面积最小。
这是因为,表面能正比于面积。
下面咱们展开来看一看这其中的关系。
单位中蕴含重要原理
表面张力的单位为【N/m】,经过换算,我们发现【N/m】=【J/m^2】。
从这个等价单位可以看出,表面张力其实是“单位面积上的能量”。即:
表面张力=表面能密度
这样,我们就更容易理解公式——
表面能[J]=表面张力[N/m]×面积[m^2]
其实就是——
表面能[J]=表面能密度[J/m^2]×面积[m^2]
以上其实是“量纲分析”的一种典型应用,为了简单,采用“单位”的方式叙述,其实道理是一样的。
拓展:压强就是压力能密度
由以上分析,我们可以想到,压强的单位——
【Pa】=【N/m^2】=【J/m^3】
是否有所启发?
是的。压强,其实就是压力能(储存于三维体)的密度。
对应的,表面张力,是表面能(储存于二维面)的密度。
还记得流体力学中的"静力学方程"吗——
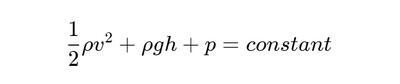
其实就是单位体积的能量守恒——动能+重力势能+压力能为常量。
再拓展:表面张力是强度量
物理量分两类:强度量(intensive quantity)与广延量(extensive quantity)。
强度量是指与体系质量无关的量,如应力、压强、密度、温度、比热、表面能密度(表面张力)等。
广延量就是与体系质量成正比的量,如体积、内能、面积、质量、熵、电量、表面能等。

换种思考,强度量不具有可加性,广延量具有可加性。
比如说,温度加温度是什么?没有物理意义呀。
两者的关系是——
广延量=强度量×体系的量
需要提醒的是,我们已经知道——
表面能密度[J/m^2]=表面张力[N/m]
表面能[J]=表面张力[N/m]×面积[m^2]
不过,大量的中文文献和书籍中,经常用“表面能”来代替“表面能密度”,阅读时需要注意。
压强与表面张力的关系
先做一个小实验:咱们拿一个"铁丝圆环",从肥皂水里蘸一下,取出后会形成一个非常平整的薄膜。(这是因为肥皂膜自发地追求表面/表面能最小)
这时,咱们在一侧吹气(相当于施加了一个压强),平整的薄膜就发生“弯曲”——
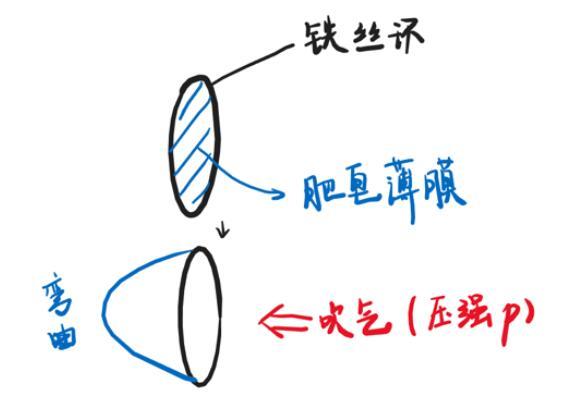
事实上,弯曲的表面与压强最终达到平衡。
那么,咱们列一下平衡方程吧(假设压强均匀、薄膜为球面)——关注黑色圆平面:
表面张力×圆周长=压强×圆面积
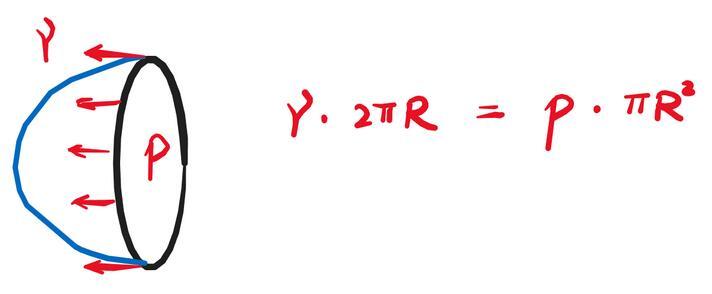
从前面的量纲分析中,我们也看到该公式的合理性,写成单位形式——
[N/m]×[m]=[N/m^2]×[m^2]
公式化简,得到——
p=2γ/R
这就是标准的球曲面下,压强与表面张力的关系。
这个公式也是【杨-拉普拉斯方程】的一种简单的形式。
还有更简单的形式
杨-拉普拉斯方程还有更简单的形式,这里需要我们了解一点关于曲率的概论。
中学时我们学过,曲率κ定义为半径的倒数,即:κ=1/R。
这其实是二维下的特殊情况。
对于三维曲面,曲率等于任意两个垂直方向上的曲率之和——
显然,标准球曲面的曲率κ=2/R。
下面不用我说大家也知道如何化简了——
p=γ·κ
这里的p,可以理解为由于表面的出现,而产生的“附加压强”,这个压强的大小与正负,与曲率直接相关。
如下图,无论是液体中的气泡,还是气体中的液滴,只要是球内的部分,压强就要比球外大,这是由于曲率的正负决定的。
这里科技千里眼奉送一个自己做的仿真计算——液滴在表面张力作用下的变形,我们看到,蓝色部分为负曲率,因此压强为负,而红色部分为正曲率,因此压强为正,液体会从正压强流向负压强,这也是表面张力影响下流体变形的基本原理。
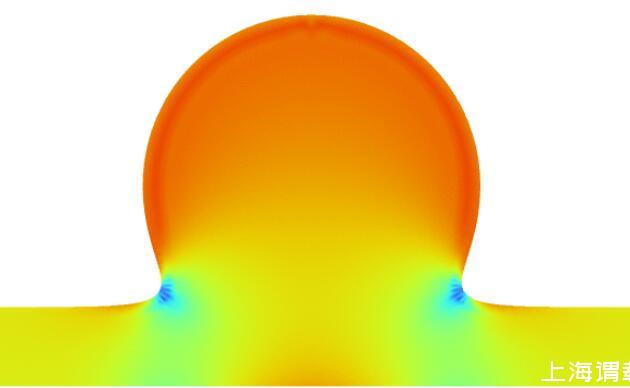
由公式p=γ·κ想到的
液滴(气泡)半径越小,压强越大,它向周边溶解气体的速率就越快;历经一段时间后,小气泡会逐渐消失,聚集成大气泡,这是气泡的【演变动力学】——

有没有这种情况,就是液滴(气泡)半径无限小,那么,我们是不是创造了一个无限大的压强呢?
比如,当液滴(气泡)刚刚形成时,不就是这种情况吗?
但是,我们也知道,自然界是不会存在无限大的压强的。这是怎么回事呢?
原来,液滴或气泡的形成,是需要一个微小的异物(核)的,一般是灰尘;如果水凝聚在灰尘颗粒上,液滴就能够长大。
对于气泡来说,也类似,一些碳酸饮料中,气体的胚胎残留在瓶壁上的某些位置,这些位置正是极微小的凸凹不平处,它们使得气泡不断长大。











