摩登7平台合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
-
> 脱模剂配方中加入石油磺酸钠,可降低液体表面张力、减少界面形成
> 各种测量ILs汽化焓对比:表面张力法、热重法、简单相加法、 基团贡献法……(一)
> 10种常用表面活性剂水溶液的表面张力测定、泡沫的产生和测试(二)
> 水面上单分子层膜通过磷脂光控开关实现可逆光学控制——实验
> 表面能和表面张力关系,如何降低表面张力
> Delta-8 动物胃肠道体内中药物的溶解度的测定——结论、工具书类!
> 如何判断表面张力仪的好坏?
> 植物油中N-酰基氨基酸表面活性剂的界面活性和聚集行为——摘要、简介
> 影响狭缝间氢键流体气液平衡界面张力的因素有哪些(二)
> 一种新表面张力改性方法让全固态电池性能更优
推荐新闻Info
-
> 不同PQAI溶液静态/动态表面张力变化及对脉动热管性能影响(三)
> 不同PQAI溶液静态/动态表面张力变化及对脉动热管性能影响(二)
> 不同PQAI溶液静态/动态表面张力变化及对脉动热管性能影响(一)
> 界面流变仪可以测量液体表面张力吗?界面流变仪与界面张力仪区别解析
> 测量表面张力/界面张力的仪器有哪些?怎么选
> PG脱酰胺添加量对玉米醇溶蛋白气-水动态表面张力的影响
> 摩登7表面张力仪使用指南【专业版】
> 平面流动皂膜表面张力系数、厚度和流动速度实验装置及测量方法(二)
> 平面流动皂膜表面张力系数、厚度和流动速度实验装置及测量方法(一)
> 单层膜界面上亚微米颗粒表面张力阻力系数修正——颗粒在单层膜上的阻力系数
探讨一级相变过程中气泡和液滴临界半径的变化规律、演化方向(二)
来源:大学物理 浏览 1017 次 发布时间:2024-09-23
由于热涨落将产生一系列气泡或液滴,此处仅考虑某一气泡或液滴,并以其产生位置的中心作为坐标系原点。考虑到相变发生前的背景环境以及原点处的非奇异性要求,设置气泡解的边界条件σr=∞=σ0及dr|r=0=0,以及液滴解的边界条件σr=∞=σv及dσdr|r=0=0,可对式(10)中σ场运动方程进行严格的数值求解。在固定化学势μ=0 MeV的情况下,设定温度T=90.0,110.0,115.0,118.0及119.5 MeV绘制了对应前者在夸克的液相背景中产生强子气相的气泡解如图2(a),以及设定温度T=130.0,128.0,127.0,126.5及126.3 MeV绘制后者在强子的气相背景中产生夸克液相的液滴解如图2(b)。
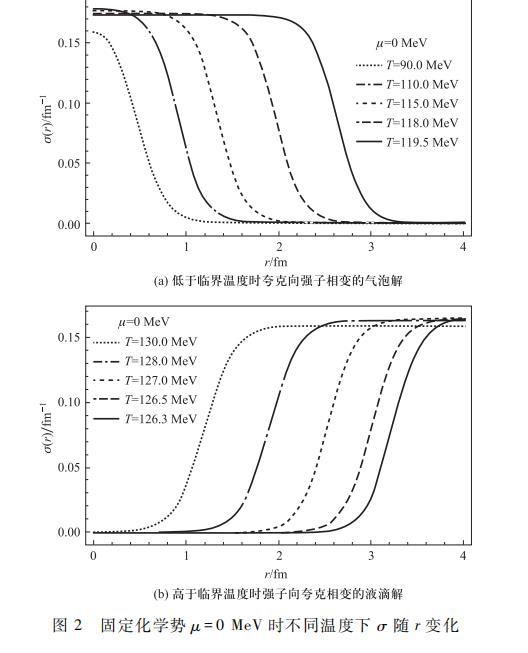
由图2(a)可看出,不同温度下会产生一系列夸克到强子相变的气泡解,曲线拐点处可看做气泡的半径,大致可以认为是气泡在此温度下的临界半径。从图中可以看出随着温度的升高而逐渐靠近相变临界温度气泡解的半径逐渐变大,并且在接近临界温度时气泡解半径增加随温度增加的变化率明显大于远离临界温度时气泡半径随温度的变化率。这说明系统在靠近临界温度时,气泡的临界半径会急速增加,但是这并不表示此时系统中已经产生了越来越大的气泡,恰恰相反,在气泡临界半径越大时,系统中越难以产生气泡,这是由于存在着气泡体积能和表面张力的竞争,对于一定临界半径的气泡代表着收缩与膨胀达到平横时的气泡,系统通常会由于热涨落而产生大小不一的气泡,对于临界半径很大时只有很小概率的随机产生的气泡半径可能大于此时临界半径而继续膨胀下去,而大概率的随机产生的气泡都小于此时临界半径将会继续收缩而消失。但当温度逐渐降低,气泡的临界半径减小,将会存在越来越大的概率产生半径大于临界半径的气泡,这些气泡发生膨胀并且彼此之间相互合并,最终充满整个空间完成相变过程。本文对于气泡解的数值结果与以往文献中的结果一致。
反过来,图2(b)所示的液滴解中同样可做类似讨论。液滴解曲线的拐点处也可以粗略看做液滴的临界半径,随着温度的逐渐降低而靠近相变临界温度,液滴解的半径逐渐增加,同样在接近临界温度处液滴解随温度的变化明显大于远离临界温度处时的变化。这就是说,在强子背景中产生了许多大小不一的夸克液滴,当温度靠近临界温度时,由于此时对应液滴的临界半径较大,因此许多随机产生的液滴难以达到临界液滴的半径就在产生后在表面张力作用下收缩消失了;但当温度逐渐升高,液滴的临界半径减小,将会存在越来越多随机产生的半径大于临界半径的液滴,这些液滴发生膨胀并彼此间相互合并最终充满整个空间完成相变过程。
进一步,本文对式(12)、(16)进行了数值求解,得到了气泡解和液滴解的表面张力及临界半径在μ=0 MeV时随温度变化的曲线,如图3和4.式(10)是非线性方程,难以解析求解。以往研究者的文章中曾利用薄壁近似进行解析求解进而得到气泡表面张力随温度减小而单调减小的结果。但本文的数值结果图3(a)表明,在温度从临界温度开始减小时,表面张力会先增加。当温度到达T=109 MeV附近时,表面张力达最大值,然后再随温度减小而单调减小。而我们知道严格来说薄壁近似只在临界温度处适用,这里表面张力的非单调变化表明在偏离临界温度时,薄壁近似结果是会明显偏离严格数值计算结果的。这一结果与以往研究者结果是一致的。
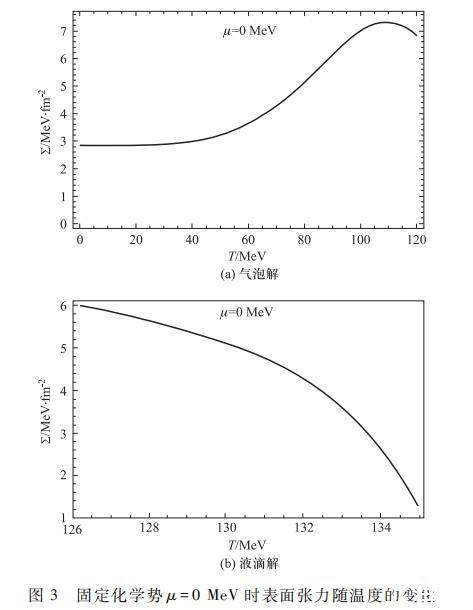
限于数值计算的能力,在非常接近临界温度时的液滴解难以求解,本文仅给出相对接近临界温度的一段数值结果。由绘制的图像可以看出,与气泡解类似,液滴表面张力随温度逐渐接近临界温度而单调增加,在这段温度范围内,定性上本文数值结果与以往研究者在薄壁近似下所得到的解析结果一致。
值得指出的是,对于液滴解,由图1可以看出在更高温度时,在σ=σv处的极小值将会消失,即伪真空消失。此时全空间将是均匀的夸克相,相变已经完成,液滴解也随之消失,所以在更高温度区域不存在液滴解。
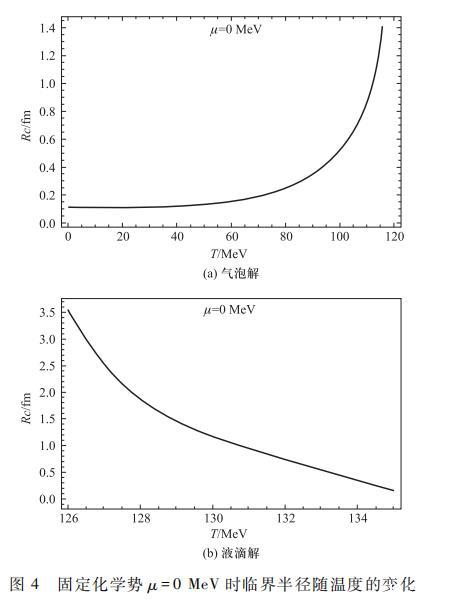
对于临界半径Rc随温度的变化可参见图4,在远离临界温度Tc时,气泡和液滴的Rc都从一个较小值,随温度靠近Tc的方向较为平缓地增加。但随着温度接近Tc,Rc随温度的变化将越来越迅速。这意味着在接近临界温度的时候,相对远离临界温度处,由于临界半径Rc迅速变大,使得系统难以产生R>;Rc的气泡或液滴。从气泡动力学的角度来看,虽然理论上Tc是相变的临界温度,但是此时的状态只是对应相变刚刚开始的状态,还很难产生气泡或液滴来推动两相的转换,只有继续适当降温或升温时,才使得系统中更有可能产生大于临界半径的气泡或液滴,从而驱动相变进行并导致最终两相的转换。
最后我们研究一下气泡和液滴的成核率Γ以及ΔFb/T的变化规律。结合式(11)和(17)可以数值计算出相应气泡和液滴成核率Γ以及ΔFb/T如图5、6所示。需要强调,虽然图4的数值结果显示临界半径随温度降低而下降,但由于式(17)中成核率并不具备与温度的简单关系,因此不能简单认为由于临界半径随温度降低而下降,从而成核率也会单调下降或上升,而是需要综合考虑图6数值结果以及不同温度下因子P对成核率的贡献。从图5可以看出,气泡的成核率在临界温度处接近0,随着温度下降,成核率的数值突然上升,在达到一个极值后,成核率随温度下降而逐渐减小,可以看到在临界温度以下成核率随温度是非单调变化的。而液滴解在临界温度以上,在所考虑的温度范围内,从临界温度开始成核率随着温度的升高而单调上升,这是由于温度升高和ΔFb/T的单调减小所造成的效应都是使成核率单调增加的。
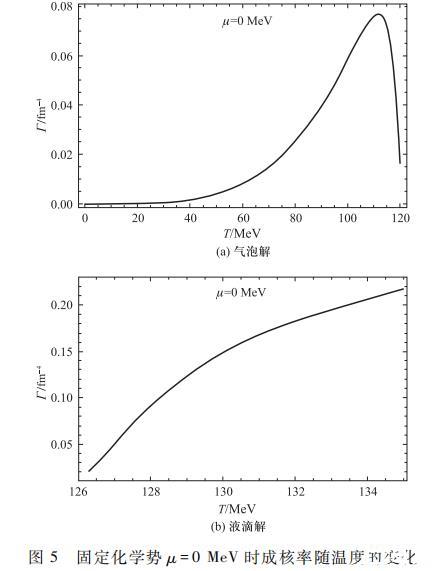
另外,我们也计算了薄壁近似下成核率的结果,所得到的结果与此处严格数值计算结果只在定量上存在差别,而成核率薄壁近似的结果和严格计算的结果在定性的变化趋势上是基本一致的。另外,从图6可以看出ΔFb/T的变化,对于气泡解,在临界温度附近,随着温度靠近临界温度,ΔFb/T的值将迅速增大,而当温度远离临界温度时,ΔFb/T的值逐渐减小,但是在靠近零温时,ΔFb/T的值又会迅速变大。
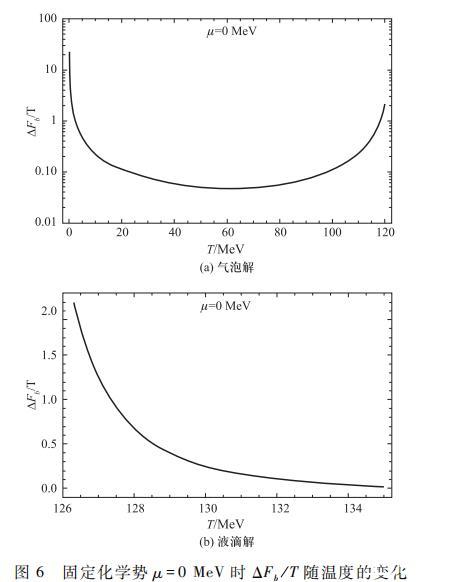
对于液滴解,ΔFb/T的值在靠近临界温度时也是迅速增加,而当温度远离临界温度时逐渐减小。造成这两者变化的主要不同在于亚稳态是否会消失,对于气泡解从图1有效势的变化可以看出即使到零温,亚稳态仍然不会消失,所以ΔFb/T的值会在接近零温时快速变大并趋于发散,但是从描述相变的角度来看远离临界温度的气泡解已经不再具有真实的物理意义。这与以往文献中对于此模型研究的数值结果是一致的。而对于液滴解情形有效势亚稳态会在温度升高到Tsp=142.8 MeV时消失,Tsp这个温度称为亚稳态分解(Spinodal)温度,此时液滴解不再存在,ΔFb/T的值变为0.
特别需要说明的是在临界温度附近,当式(17)中的指数部分ΔFb/T≌1时对应的温度在一级相变的过程中具有重要意义,其标示了亚稳相真正向稳定相发生实际转变的开始。以气泡解为例,当ΔFb/T≌1时,Γ的指数项变为1/e,此时对应的温度为T1=118.1 MeV,这说明在Tc=119.8 MeV和T1=118.1 MeV之间系统能够在相对长的时间内保持在夸克相亚稳态。但当温度进一步降低时,夸克相亚稳态才会实际上通过气泡动力学过程快速地向稳定强子相转变,即液相背景中快速产生强子气泡并迅速膨胀合并从而完成相变过程。液滴解中的物理过程完全类似,液滴解在T2=127.3 MeV时有ΔFb/T≌1,表明在Tc=119.8 MeV和T2=127.3 MeV之间系统能够在相对长的时间内保持在强子相亚稳态,只有当温度进一步升高到超过T2=127.3 MeV时,系统将通过液滴成核的动力学过程快速向夸克相转变。当温度升高至Tsp=142.8 MeV时,强子的亚稳态真空完全消失,如果此时相变还没有全部完成,那么系统会发生剧烈的强子相到夸克相的转变过程。
3、总结与展望
本文主要讨论了夸克物质系统在发生一级相变过程中的气泡或液滴动力学问题。具体从F-L模型出发,理论推导得出σ场运动方程以及表面张力、临界半径等物理量的表达式,并利用数值方法计算了相关物理量的严格数值解,同时结合薄壁近似讨论了气泡和液滴临界半径的变化规律。根据气泡或液滴核合成唯象模型,将相变过程看做亚稳态真空背景中产生的稳定真空的气泡或液滴,通过数值计算具体分析了所得气泡和液滴解结果的物理意义,并阐明了在相变过程中气泡或液滴的演化作为一种动力学机制驱动相变的物理图像。同时,根据成核率相关的数值结果,求解了相变过程中系统气泡或液滴解在ΔFb/T=1时的温度,并分析了对应的物理意义。相对前人的工作,本文主要强调了一级相变过程中热力学系统朝向低温和高温不同方向演化时,会存在着气泡解和液滴解的不同,并且清晰的给出了两种解的物理图像和相关性质的对比,在求解计算中主要采用动力学场方程的严格数值解,弱化了薄壁近似的使用。
本文虽然只在有限温度下讨论了气泡或液滴的动力学问题,但是这里给出的分析方法同样可以推广到有限密度的情形。F-L模型只能给出一级相变结果,本文的结果具有一定模型依赖性,对于重离子碰撞所产生的包含平滑过渡的实际系统来讲还不能很好的描述。因此接下来的研究中,希望能够将本文工作推广至同时具有手征对称性和禁闭特征的QCD有效模型中,例如Polyakov-quark-meson model(PQM)模型,从而能讨论在有限密度下更加接近实际情形的系统中一级相变过程中的气泡或液滴的动力学问题,并期望能对重离子碰撞中夸克物质相变的相临界点研究以及中子星形成过程中的内部结构研究提供一定的理论参考。










